ESTRUTURAS METÁLICAS E DE MADEIRA
De acordo com a ABNT NBR 7190:1997, é possível classificar as peças comprimidas de madeira segundo o valor do índice de esbeltez λ:
1- λ ≤ 40
2- 40 < λ ≤ 80
3- 80 < λ ≤ 140
Qual a ordem correta dessas classificações?
1- Peças medianamente esbeltas; 2- Peças esbeltas; 3- Peças curtas.
1- Peças curtas; 2- Peças esbeltas; 3- Peças medianamente esbeltas.
1- Peças esbeltas; 2- Peças medianamente esbeltas; 3- Peças curtas.
1- Peças curtas; 2- Peças medianamente esbeltas; 3- Peças esbeltas.
1- Peças esbeltas; 2- Peças curtas; 3- Peças medianamente esbeltas.
Segundo a ABNT NBR 7190:1997, quais os valores mínimos esperados para as espessuras das peças de madeira em uma ligação pregada de corte simples, em função do diâmetro (d) do prego?
Assumindo que t é a menor espessura de penetração do pino e def = d0.
t = 5d e t4 = 12d.
t = 12d e t4 = 5d.
t = 12d e t4 = 4d.
t = 4d e t4 = 12d.
t = 5d e t4 = 5d.
Obter a resistência de cálculo no estado limite último da madeira Pinus taeda (conífera) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 3 e madeira serrada de 1ª categoria. Valores médios adotados:
fc0,m = 44,4 MPa
Ec0,m = 13 304 MPa
Em caso de resposta decimal, considerar uma casa após a vírgula.
fc0,d = 9,9 MPa; Ec0,ef = 5960,2 MPa.
fc0,d = 12,4 MPa; Ec0,ef = 7450,2 MPa.
fc0,d = 13,2 MPa; Ec0,ef = 6346,9 MPa.
fc0,d = 24,3 MPa; Ec0,ef = 8068,9 MPa.
fc0,d = 17,02 MPa; Ec0,ef = 10086,1 MPa.
Determinar a resistência de cálculo no estado limite último da madeira Cupiúba (dicotiledônea) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 2 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 54,4 MPa
Ec0,m = 13627 MPa
fc0,d = 38,08 MPa; Ec0,d = 13627 MPa.
fc0,d = 12,19 MPa; Ec0,d = 6104,9 MPa.
fc0,d = 17,41 MPa; Ec0,d = 6104,9 MPa.
fc0,d = 15,23 MPa; Ec0,d = 7631,12 MPa.
fc0,d = 30,46 MPa; Ec0,d = 7631,12 MPa.
A determinação da força crítica de flambagem é um procedimento muito importante para analisar o comportamento de estruturas sujeitas à compressão, como pilares e arcos. É com base no valor da força crítica de flambagem que é possível identificar inicialmente se o equilíbrio da estrutura será estável, neutro ou instável conforme as ações suportadas. Curiosamente, o conceito de força crítica de flambagem foi primeiramente desenvolvido por Euler ainda no século XVIII, quando o emprego de peças estruturais esbeltas ainda não era comum, pois somente com a revolução industrial e o advento do aço estrutural houve a objetivo de priorizar a esbeltez das estruturas. É possível afirmar que a contribuição de Euler para a engenharia estrutural foi essencial e muito à frente de seu tempo.
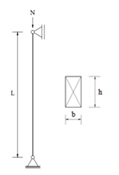
Dessa forma, determine a força crítica de flambagem (Fe) para o pilar de madeira indicado. O pilar é simplesmente apoiado segundo os dois planos de análise. A seção transversal é retangular, base (b) de 6 cm e altura (h) de 16 cm. A barra possui comprimento (L) de 235 cm. Considerar madeira dicotiledônea serrada de 2ª categoria, classe de resistência C60, classe de carregamento de longa duração e classe de umidade 2.
Em caso de resposta decimal, considerar uma casa após a vírgula.
Fe = 30,7 kN.
Fe = 38,1 kN.
Fe = 88,3 kN.
Fe = 70,6 kN.
Fe = 21,44 kN.
Determinar o esforço normal de tração resistente para uma barra de madeira com seção transversal retangular, com dimensões 6 × 12, segundo os requisitos de segurança quanto ao Estado Limite Último (ELU). A madeira utilizada é dicotiledônea e serrada de 2ª categoria, com classe de resistência C60. Considerar classe de carregamento de longa duração e classe de umidade 1.
Em caso de resposta decimal, considerar uma casa após a vírgula.
Nd,res = 122,9 kN.
Nd,res = 57,6 kN.
Nd,res = 144,3 kN.
Nd,res = 172,8 kN.
Nd,res = 49,2 kN.
Calcular as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça de madeira submetida à solicitação axial de tração, cujo esforço é originado a partir das seguintes ações características:
Peso próprio da estrutura de madeira: G = 21 kN (grande variabilidade)
Carga acidental (de uso e ocupação): Q = 25 kN
Ação do vento de sobrepressão: Qv1 = 17 kN
Ação do vento de sucção: Qv2 = -12 kN
Considerar que, na construção, há predominância de pesos e de equipamentos que permanecem fixos por longos períodos de tempo.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)?
76,3 kN
97,3 kN
124,5 kN
56,6 kN
106,4 kN
Determine, de acordo com a ABNT NBR 8800:2008, o esforço normal de compressão resistente de cálculo (Nd,res) para a coluna soldada (CS) indicada na figura abaixo, cujo comprimento (L) é de 4,5 m. A coluna é simplesmente apoiada em relação aos dois eixos de análise.
Aço A-36 (MR250) – Propriedades: fy = 25 kN/cm2; fu = 40 kN/cm2; E = 20000 kN/cm2.
Perfil CS 650x345 kg/m – Propriedades:
d = 650 mm
h = 600 mm
tw = 19,0 mm
tf = 25,0 mm
bf = 650 mm

Em caso de resposta decimal, arredondar o número conforme o inteiro mais próximo.
Nd,res = 13660 kN
Nd,res = 9572 kN
Nd,res = 15295 kN
Nd,res = 8270 kN
Nd,res = 12873 kN
Determine, de acordo com a ABNT NBR 8800:2008, o esforço normal de compressão resistente de cálculo (Nd,res) para a coluna soldada (CS) indicada na figura abaixo, cujo comprimento (L) é de 3 m. A coluna é simplesmente apoiada em relação aos dois eixos de análise.
Aço A-36 (MR250) Propriedades: fy = 25 kN/cm2; fu = 40 kN/cm2; E = 20000 kN/cm2.
Perfil CS 700x458 kg/m Propriedades:
d = 700 mm
h = 637 mm
tw = 22,4 mm
tf = 31,5 mm
bf = 700 mm

Em caso de resposta decimal, arredondar o número conforme o inteiro mais próximo.
Nd,res = 13060 kN
Nd,res = 15780 kN
Nd,res = 10147 kN
Nd,res = 14373 kN
Nd,res = 12032 kN
Calcular a resistência de projeto (Rd) ao corte da ligação com parafuso de 19 mm diâmetro, que liga duas peças tracionadas de madeira eucalipto citriodora, conforme recomendações da ABNT NBR 7190:1997. Considerar classe de carregamento de longa duração, classe 2 de umidade e madeira serrada de 2ª categoria. Atribuir o valor característico da resistência à compressão paralela às fibras (fc0,k) do eucalipto critiodora como 43,4 MPa, e o valor característico da resistência ao escoamento do parafuso como 240 MPa.
Adotar:
d = 19 mm.
t1 = 40 mm.
t2 = 60 mm.
2- 40 < λ ≤ 80
3- 80 < λ ≤ 140
1- Peças medianamente esbeltas; 2- Peças esbeltas; 3- Peças curtas.
1- Peças curtas; 2- Peças esbeltas; 3- Peças medianamente esbeltas.
1- Peças esbeltas; 2- Peças medianamente esbeltas; 3- Peças curtas.
1- Peças curtas; 2- Peças medianamente esbeltas; 3- Peças esbeltas.
1- Peças esbeltas; 2- Peças curtas; 3- Peças medianamente esbeltas.
Segundo a ABNT NBR 7190:1997, quais os valores mínimos esperados para as espessuras das peças de madeira em uma ligação pregada de corte simples, em função do diâmetro (d) do prego?
Assumindo que t é a menor espessura de penetração do pino e def = d0.

t = 5d e t4 = 12d.
t = 12d e t4 = 5d.
t = 12d e t4 = 4d.
t = 4d e t4 = 12d.
t = 5d e t4 = 5d.
Obter a resistência de cálculo no estado limite último da madeira Pinus taeda (conífera) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 3 e madeira serrada de 1ª categoria. Valores médios adotados:
fc0,m = 44,4 MPa
Ec0,m = 13 304 MPa
Em caso de resposta decimal, considerar uma casa após a vírgula.
fc0,d = 9,9 MPa; Ec0,ef = 5960,2 MPa.
fc0,d = 12,4 MPa; Ec0,ef = 7450,2 MPa.
fc0,d = 13,2 MPa; Ec0,ef = 6346,9 MPa.
fc0,d = 24,3 MPa; Ec0,ef = 8068,9 MPa.
fc0,d = 17,02 MPa; Ec0,ef = 10086,1 MPa.
Determinar a resistência de cálculo no estado limite último da madeira Cupiúba (dicotiledônea) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 2 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 54,4 MPa
Ec0,m = 13627 MPa
fc0,d = 38,08 MPa; Ec0,d = 13627 MPa.
fc0,d = 12,19 MPa; Ec0,d = 6104,9 MPa.
fc0,d = 17,41 MPa; Ec0,d = 6104,9 MPa.
fc0,d = 15,23 MPa; Ec0,d = 7631,12 MPa.
fc0,d = 30,46 MPa; Ec0,d = 7631,12 MPa.
A determinação da força crítica de flambagem é um procedimento muito importante para analisar o comportamento de estruturas sujeitas à compressão, como pilares e arcos. É com base no valor da força crítica de flambagem que é possível identificar inicialmente se o equilíbrio da estrutura será estável, neutro ou instável conforme as ações suportadas. Curiosamente, o conceito de força crítica de flambagem foi primeiramente desenvolvido por Euler ainda no século XVIII, quando o emprego de peças estruturais esbeltas ainda não era comum, pois somente com a revolução industrial e o advento do aço estrutural houve a objetivo de priorizar a esbeltez das estruturas. É possível afirmar que a contribuição de Euler para a engenharia estrutural foi essencial e muito à frente de seu tempo.
Dessa forma, determine a força crítica de flambagem (Fe) para o pilar de madeira indicado. O pilar é simplesmente apoiado segundo os dois planos de análise. A seção transversal é retangular, base (b) de 6 cm e altura (h) de 16 cm. A barra possui comprimento (L) de 235 cm. Considerar madeira dicotiledônea serrada de 2ª categoria, classe de resistência C60, classe de carregamento de longa duração e classe de umidade 2.
Em caso de resposta decimal, considerar uma casa após a vírgula.

Fe = 30,7 kN.
Fe = 38,1 kN.
Fe = 88,3 kN.
Fe = 70,6 kN.
Fe = 21,44 kN.
Determinar o esforço normal de tração resistente para uma barra de madeira com seção transversal retangular, com dimensões 6 × 12, segundo os requisitos de segurança quanto ao Estado Limite Último (ELU). A madeira utilizada é dicotiledônea e serrada de 2ª categoria, com classe de resistência C60. Considerar classe de carregamento de longa duração e classe de umidade 1.
Em caso de resposta decimal, considerar uma casa após a vírgula.
Nd,res = 122,9 kN.
Nd,res = 57,6 kN.
Nd,res = 144,3 kN.
Nd,res = 172,8 kN.
Nd,res = 49,2 kN.
Calcular as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça de madeira submetida à solicitação axial de tração, cujo esforço é originado a partir das seguintes ações características:
Peso próprio da estrutura de madeira: G = 21 kN (grande variabilidade)
Carga acidental (de uso e ocupação): Q = 25 kN
Ação do vento de sobrepressão: Qv1 = 17 kN
Ação do vento de sucção: Qv2 = -12 kN
Considerar que, na construção, há predominância de pesos e de equipamentos que permanecem fixos por longos períodos de tempo.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)?
76,3 kN
97,3 kN
124,5 kN
56,6 kN
106,4 kN
Determine, de acordo com a ABNT NBR 8800:2008, o esforço normal de compressão resistente de cálculo (Nd,res) para a coluna soldada (CS) indicada na figura abaixo, cujo comprimento (L) é de 4,5 m. A coluna é simplesmente apoiada em relação aos dois eixos de análise.
Aço A-36 (MR250) – Propriedades: fy = 25 kN/cm2; fu = 40 kN/cm2; E = 20000 kN/cm2.
Perfil CS 650x345 kg/m – Propriedades:
d = 650 mm
h = 600 mm
tw = 19,0 mm
tf = 25,0 mm
bf = 650 mm

Em caso de resposta decimal, arredondar o número conforme o inteiro mais próximo.
Nd,res = 13660 kN
Nd,res = 9572 kN
Nd,res = 15295 kN
Nd,res = 8270 kN
Nd,res = 12873 kN
Determine, de acordo com a ABNT NBR 8800:2008, o esforço normal de compressão resistente de cálculo (Nd,res) para a coluna soldada (CS) indicada na figura abaixo, cujo comprimento (L) é de 3 m. A coluna é simplesmente apoiada em relação aos dois eixos de análise.
Aço A-36 (MR250) Propriedades: fy = 25 kN/cm2; fu = 40 kN/cm2; E = 20000 kN/cm2.
Perfil CS 700x458 kg/m Propriedades:
d = 700 mm
h = 637 mm
tw = 22,4 mm
tf = 31,5 mm
bf = 700 mm

Em caso de resposta decimal, arredondar o número conforme o inteiro mais próximo.
Nd,res = 13060 kN
Nd,res = 15780 kN
Nd,res = 10147 kN
Nd,res = 14373 kN
Nd,res = 12032 kN
Calcular a resistência de projeto (Rd) ao corte da ligação com parafuso de 19 mm diâmetro, que liga duas peças tracionadas de madeira eucalipto citriodora, conforme recomendações da ABNT NBR 7190:1997. Considerar classe de carregamento de longa duração, classe 2 de umidade e madeira serrada de 2ª categoria. Atribuir o valor característico da resistência à compressão paralela às fibras (fc0,k) do eucalipto critiodora como 43,4 MPa, e o valor característico da resistência ao escoamento do parafuso como 240 MPa.
Adotar:
d = 19 mm.
t1 = 40 mm.
t2 = 60 mm.


t = 5d e t4 = 12d.
t = 12d e t4 = 5d.
t = 12d e t4 = 4d.
t = 4d e t4 = 12d.
t = 5d e t4 = 5d.
Obter a resistência de cálculo no estado limite último da madeira Pinus taeda (conífera) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 3 e madeira serrada de 1ª categoria. Valores médios adotados:
fc0,m = 44,4 MPa
Ec0,m = 13 304 MPa
Em caso de resposta decimal, considerar uma casa após a vírgula.
fc0,d = 9,9 MPa; Ec0,ef = 5960,2 MPa.
fc0,d = 12,4 MPa; Ec0,ef = 7450,2 MPa.
fc0,d = 13,2 MPa; Ec0,ef = 6346,9 MPa.
fc0,d = 24,3 MPa; Ec0,ef = 8068,9 MPa.
fc0,d = 17,02 MPa; Ec0,ef = 10086,1 MPa.
Determinar a resistência de cálculo no estado limite último da madeira Cupiúba (dicotiledônea) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 2 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 54,4 MPa
Ec0,m = 13627 MPa
fc0,d = 38,08 MPa; Ec0,d = 13627 MPa.
fc0,d = 12,19 MPa; Ec0,d = 6104,9 MPa.
fc0,d = 17,41 MPa; Ec0,d = 6104,9 MPa.
fc0,d = 15,23 MPa; Ec0,d = 7631,12 MPa.
fc0,d = 30,46 MPa; Ec0,d = 7631,12 MPa.
A determinação da força crítica de flambagem é um procedimento muito importante para analisar o comportamento de estruturas sujeitas à compressão, como pilares e arcos. É com base no valor da força crítica de flambagem que é possível identificar inicialmente se o equilíbrio da estrutura será estável, neutro ou instável conforme as ações suportadas. Curiosamente, o conceito de força crítica de flambagem foi primeiramente desenvolvido por Euler ainda no século XVIII, quando o emprego de peças estruturais esbeltas ainda não era comum, pois somente com a revolução industrial e o advento do aço estrutural houve a objetivo de priorizar a esbeltez das estruturas. É possível afirmar que a contribuição de Euler para a engenharia estrutural foi essencial e muito à frente de seu tempo.
Dessa forma, determine a força crítica de flambagem (Fe) para o pilar de madeira indicado. O pilar é simplesmente apoiado segundo os dois planos de análise. A seção transversal é retangular, base (b) de 6 cm e altura (h) de 16 cm. A barra possui comprimento (L) de 235 cm. Considerar madeira dicotiledônea serrada de 2ª categoria, classe de resistência C60, classe de carregamento de longa duração e classe de umidade 2.
Em caso de resposta decimal, considerar uma casa após a vírgula.

Fe = 30,7 kN.
Fe = 38,1 kN.
Fe = 88,3 kN.
Fe = 70,6 kN.
Fe = 21,44 kN.
Determinar o esforço normal de tração resistente para uma barra de madeira com seção transversal retangular, com dimensões 6 × 12, segundo os requisitos de segurança quanto ao Estado Limite Último (ELU). A madeira utilizada é dicotiledônea e serrada de 2ª categoria, com classe de resistência C60. Considerar classe de carregamento de longa duração e classe de umidade 1.
Em caso de resposta decimal, considerar uma casa após a vírgula.
Nd,res = 122,9 kN.
Nd,res = 57,6 kN.
Nd,res = 144,3 kN.
Nd,res = 172,8 kN.
Nd,res = 49,2 kN.
Calcular as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça de madeira submetida à solicitação axial de tração, cujo esforço é originado a partir das seguintes ações características:
Peso próprio da estrutura de madeira: G = 21 kN (grande variabilidade)
Carga acidental (de uso e ocupação): Q = 25 kN
Ação do vento de sobrepressão: Qv1 = 17 kN
Ação do vento de sucção: Qv2 = -12 kN
Considerar que, na construção, há predominância de pesos e de equipamentos que permanecem fixos por longos períodos de tempo.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)?
76,3 kN
97,3 kN
124,5 kN
56,6 kN
106,4 kN
Determine, de acordo com a ABNT NBR 8800:2008, o esforço normal de compressão resistente de cálculo (Nd,res) para a coluna soldada (CS) indicada na figura abaixo, cujo comprimento (L) é de 4,5 m. A coluna é simplesmente apoiada em relação aos dois eixos de análise.
Aço A-36 (MR250) – Propriedades: fy = 25 kN/cm2; fu = 40 kN/cm2; E = 20000 kN/cm2.
Perfil CS 650x345 kg/m – Propriedades:
d = 650 mm
h = 600 mm
tw = 19,0 mm
tf = 25,0 mm
bf = 650 mm

Em caso de resposta decimal, arredondar o número conforme o inteiro mais próximo.
Nd,res = 13660 kN
Nd,res = 9572 kN
Nd,res = 15295 kN
Nd,res = 8270 kN
Nd,res = 12873 kN
Determine, de acordo com a ABNT NBR 8800:2008, o esforço normal de compressão resistente de cálculo (Nd,res) para a coluna soldada (CS) indicada na figura abaixo, cujo comprimento (L) é de 3 m. A coluna é simplesmente apoiada em relação aos dois eixos de análise.
Aço A-36 (MR250) Propriedades: fy = 25 kN/cm2; fu = 40 kN/cm2; E = 20000 kN/cm2.
Perfil CS 700x458 kg/m Propriedades:
d = 700 mm
h = 637 mm
tw = 22,4 mm
tf = 31,5 mm
bf = 700 mm

Em caso de resposta decimal, arredondar o número conforme o inteiro mais próximo.
Nd,res = 13060 kN
Nd,res = 15780 kN
Nd,res = 10147 kN
Nd,res = 14373 kN
Nd,res = 12032 kN
Calcular a resistência de projeto (Rd) ao corte da ligação com parafuso de 19 mm diâmetro, que liga duas peças tracionadas de madeira eucalipto citriodora, conforme recomendações da ABNT NBR 7190:1997. Considerar classe de carregamento de longa duração, classe 2 de umidade e madeira serrada de 2ª categoria. Atribuir o valor característico da resistência à compressão paralela às fibras (fc0,k) do eucalipto critiodora como 43,4 MPa, e o valor característico da resistência ao escoamento do parafuso como 240 MPa.
Adotar:
d = 19 mm.
t1 = 40 mm.
t2 = 60 mm.

fc0,d = 9,9 MPa; Ec0,ef = 5960,2 MPa.
fc0,d = 12,4 MPa; Ec0,ef = 7450,2 MPa.
fc0,d = 13,2 MPa; Ec0,ef = 6346,9 MPa.
fc0,d = 24,3 MPa; Ec0,ef = 8068,9 MPa.
fc0,d = 17,02 MPa; Ec0,ef = 10086,1 MPa.
Determinar a resistência de cálculo no estado limite último da madeira Cupiúba (dicotiledônea) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 2 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 54,4 MPa
Ec0,m = 13627 MPa
fc0,d = 38,08 MPa; Ec0,d = 13627 MPa.
fc0,d = 12,19 MPa; Ec0,d = 6104,9 MPa.
fc0,d = 17,41 MPa; Ec0,d = 6104,9 MPa.
fc0,d = 15,23 MPa; Ec0,d = 7631,12 MPa.
fc0,d = 30,46 MPa; Ec0,d = 7631,12 MPa.
A determinação da força crítica de flambagem é um procedimento muito importante para analisar o comportamento de estruturas sujeitas à compressão, como pilares e arcos. É com base no valor da força crítica de flambagem que é possível identificar inicialmente se o equilíbrio da estrutura será estável, neutro ou instável conforme as ações suportadas. Curiosamente, o conceito de força crítica de flambagem foi primeiramente desenvolvido por Euler ainda no século XVIII, quando o emprego de peças estruturais esbeltas ainda não era comum, pois somente com a revolução industrial e o advento do aço estrutural houve a objetivo de priorizar a esbeltez das estruturas. É possível afirmar que a contribuição de Euler para a engenharia estrutural foi essencial e muito à frente de seu tempo.
Dessa forma, determine a força crítica de flambagem (Fe) para o pilar de madeira indicado. O pilar é simplesmente apoiado segundo os dois planos de análise. A seção transversal é retangular, base (b) de 6 cm e altura (h) de 16 cm. A barra possui comprimento (L) de 235 cm. Considerar madeira dicotiledônea serrada de 2ª categoria, classe de resistência C60, classe de carregamento de longa duração e classe de umidade 2.
Em caso de resposta decimal, considerar uma casa após a vírgula.

Fe = 30,7 kN.
Fe = 38,1 kN.
Fe = 88,3 kN.
Fe = 70,6 kN.
Fe = 21,44 kN.
Determinar o esforço normal de tração resistente para uma barra de madeira com seção transversal retangular, com dimensões 6 × 12, segundo os requisitos de segurança quanto ao Estado Limite Último (ELU). A madeira utilizada é dicotiledônea e serrada de 2ª categoria, com classe de resistência C60. Considerar classe de carregamento de longa duração e classe de umidade 1.
Em caso de resposta decimal, considerar uma casa após a vírgula.
Nd,res = 122,9 kN.
Nd,res = 57,6 kN.
Nd,res = 144,3 kN.
Nd,res = 172,8 kN.
Nd,res = 49,2 kN.
Calcular as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça de madeira submetida à solicitação axial de tração, cujo esforço é originado a partir das seguintes ações características:
Peso próprio da estrutura de madeira: G = 21 kN (grande variabilidade)
Carga acidental (de uso e ocupação): Q = 25 kN
Ação do vento de sobrepressão: Qv1 = 17 kN
Ação do vento de sucção: Qv2 = -12 kN
Considerar que, na construção, há predominância de pesos e de equipamentos que permanecem fixos por longos períodos de tempo.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)?
76,3 kN
97,3 kN
124,5 kN
56,6 kN
106,4 kN
Determine, de acordo com a ABNT NBR 8800:2008, o esforço normal de compressão resistente de cálculo (Nd,res) para a coluna soldada (CS) indicada na figura abaixo, cujo comprimento (L) é de 4,5 m. A coluna é simplesmente apoiada em relação aos dois eixos de análise.
Aço A-36 (MR250) – Propriedades: fy = 25 kN/cm2; fu = 40 kN/cm2; E = 20000 kN/cm2.
Perfil CS 650x345 kg/m – Propriedades:
d = 650 mm
h = 600 mm
tw = 19,0 mm
tf = 25,0 mm
bf = 650 mm

Em caso de resposta decimal, arredondar o número conforme o inteiro mais próximo.
Nd,res = 13660 kN
Nd,res = 9572 kN
Nd,res = 15295 kN
Nd,res = 8270 kN
Nd,res = 12873 kN
Determine, de acordo com a ABNT NBR 8800:2008, o esforço normal de compressão resistente de cálculo (Nd,res) para a coluna soldada (CS) indicada na figura abaixo, cujo comprimento (L) é de 3 m. A coluna é simplesmente apoiada em relação aos dois eixos de análise.
Aço A-36 (MR250) Propriedades: fy = 25 kN/cm2; fu = 40 kN/cm2; E = 20000 kN/cm2.
Perfil CS 700x458 kg/m Propriedades:
d = 700 mm
h = 637 mm
tw = 22,4 mm
tf = 31,5 mm
bf = 700 mm

Em caso de resposta decimal, arredondar o número conforme o inteiro mais próximo.
Nd,res = 13060 kN
Nd,res = 15780 kN
Nd,res = 10147 kN
Nd,res = 14373 kN
Nd,res = 12032 kN
Calcular a resistência de projeto (Rd) ao corte da ligação com parafuso de 19 mm diâmetro, que liga duas peças tracionadas de madeira eucalipto citriodora, conforme recomendações da ABNT NBR 7190:1997. Considerar classe de carregamento de longa duração, classe 2 de umidade e madeira serrada de 2ª categoria. Atribuir o valor característico da resistência à compressão paralela às fibras (fc0,k) do eucalipto critiodora como 43,4 MPa, e o valor característico da resistência ao escoamento do parafuso como 240 MPa.
Adotar:
d = 19 mm.
t1 = 40 mm.
t2 = 60 mm.

fc0,d = 38,08 MPa; Ec0,d = 13627 MPa.
fc0,d = 12,19 MPa; Ec0,d = 6104,9 MPa.
fc0,d = 17,41 MPa; Ec0,d = 6104,9 MPa.
fc0,d = 15,23 MPa; Ec0,d = 7631,12 MPa.
fc0,d = 30,46 MPa; Ec0,d = 7631,12 MPa.
A determinação da força crítica de flambagem é um procedimento muito importante para analisar o comportamento de estruturas sujeitas à compressão, como pilares e arcos. É com base no valor da força crítica de flambagem que é possível identificar inicialmente se o equilíbrio da estrutura será estável, neutro ou instável conforme as ações suportadas. Curiosamente, o conceito de força crítica de flambagem foi primeiramente desenvolvido por Euler ainda no século XVIII, quando o emprego de peças estruturais esbeltas ainda não era comum, pois somente com a revolução industrial e o advento do aço estrutural houve a objetivo de priorizar a esbeltez das estruturas. É possível afirmar que a contribuição de Euler para a engenharia estrutural foi essencial e muito à frente de seu tempo.
Dessa forma, determine a força crítica de flambagem (Fe) para o pilar de madeira indicado. O pilar é simplesmente apoiado segundo os dois planos de análise. A seção transversal é retangular, base (b) de 6 cm e altura (h) de 16 cm. A barra possui comprimento (L) de 235 cm. Considerar madeira dicotiledônea serrada de 2ª categoria, classe de resistência C60, classe de carregamento de longa duração e classe de umidade 2.
Em caso de resposta decimal, considerar uma casa após a vírgula.

Fe = 30,7 kN.
Fe = 38,1 kN.
Fe = 88,3 kN.
Fe = 70,6 kN.
Fe = 21,44 kN.
Determinar o esforço normal de tração resistente para uma barra de madeira com seção transversal retangular, com dimensões 6 × 12, segundo os requisitos de segurança quanto ao Estado Limite Último (ELU). A madeira utilizada é dicotiledônea e serrada de 2ª categoria, com classe de resistência C60. Considerar classe de carregamento de longa duração e classe de umidade 1.
Em caso de resposta decimal, considerar uma casa após a vírgula.
Nd,res = 122,9 kN.
Nd,res = 57,6 kN.
Nd,res = 144,3 kN.
Nd,res = 172,8 kN.
Nd,res = 49,2 kN.
Calcular as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça de madeira submetida à solicitação axial de tração, cujo esforço é originado a partir das seguintes ações características:
Peso próprio da estrutura de madeira: G = 21 kN (grande variabilidade)
Carga acidental (de uso e ocupação): Q = 25 kN
Ação do vento de sobrepressão: Qv1 = 17 kN
Ação do vento de sucção: Qv2 = -12 kN
Considerar que, na construção, há predominância de pesos e de equipamentos que permanecem fixos por longos períodos de tempo.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)?
76,3 kN
97,3 kN
124,5 kN
56,6 kN
106,4 kN
Determine, de acordo com a ABNT NBR 8800:2008, o esforço normal de compressão resistente de cálculo (Nd,res) para a coluna soldada (CS) indicada na figura abaixo, cujo comprimento (L) é de 4,5 m. A coluna é simplesmente apoiada em relação aos dois eixos de análise.
Aço A-36 (MR250) – Propriedades: fy = 25 kN/cm2; fu = 40 kN/cm2; E = 20000 kN/cm2.
Perfil CS 650x345 kg/m – Propriedades:
d = 650 mm
h = 600 mm
tw = 19,0 mm
tf = 25,0 mm
bf = 650 mm

Em caso de resposta decimal, arredondar o número conforme o inteiro mais próximo.
Nd,res = 13660 kN
Nd,res = 9572 kN
Nd,res = 15295 kN
Nd,res = 8270 kN
Nd,res = 12873 kN
Determine, de acordo com a ABNT NBR 8800:2008, o esforço normal de compressão resistente de cálculo (Nd,res) para a coluna soldada (CS) indicada na figura abaixo, cujo comprimento (L) é de 3 m. A coluna é simplesmente apoiada em relação aos dois eixos de análise.
Aço A-36 (MR250) Propriedades: fy = 25 kN/cm2; fu = 40 kN/cm2; E = 20000 kN/cm2.
Perfil CS 700x458 kg/m Propriedades:
d = 700 mm
h = 637 mm
tw = 22,4 mm
tf = 31,5 mm
bf = 700 mm

Em caso de resposta decimal, arredondar o número conforme o inteiro mais próximo.
Nd,res = 13060 kN
Nd,res = 15780 kN
Nd,res = 10147 kN
Nd,res = 14373 kN
Nd,res = 12032 kN
Calcular a resistência de projeto (Rd) ao corte da ligação com parafuso de 19 mm diâmetro, que liga duas peças tracionadas de madeira eucalipto citriodora, conforme recomendações da ABNT NBR 7190:1997. Considerar classe de carregamento de longa duração, classe 2 de umidade e madeira serrada de 2ª categoria. Atribuir o valor característico da resistência à compressão paralela às fibras (fc0,k) do eucalipto critiodora como 43,4 MPa, e o valor característico da resistência ao escoamento do parafuso como 240 MPa.
Adotar:
d = 19 mm.
t1 = 40 mm.
t2 = 60 mm.


Fe = 30,7 kN.
Fe = 38,1 kN.
Fe = 88,3 kN.
Fe = 70,6 kN.
Fe = 21,44 kN.
Determinar o esforço normal de tração resistente para uma barra de madeira com seção transversal retangular, com dimensões 6 × 12, segundo os requisitos de segurança quanto ao Estado Limite Último (ELU). A madeira utilizada é dicotiledônea e serrada de 2ª categoria, com classe de resistência C60. Considerar classe de carregamento de longa duração e classe de umidade 1.
Em caso de resposta decimal, considerar uma casa após a vírgula.
Nd,res = 122,9 kN.
Nd,res = 57,6 kN.
Nd,res = 144,3 kN.
Nd,res = 172,8 kN.
Nd,res = 49,2 kN.
Calcular as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça de madeira submetida à solicitação axial de tração, cujo esforço é originado a partir das seguintes ações características:
Peso próprio da estrutura de madeira: G = 21 kN (grande variabilidade)
Carga acidental (de uso e ocupação): Q = 25 kN
Ação do vento de sobrepressão: Qv1 = 17 kN
Ação do vento de sucção: Qv2 = -12 kN
Considerar que, na construção, há predominância de pesos e de equipamentos que permanecem fixos por longos períodos de tempo.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)?
76,3 kN
97,3 kN
124,5 kN
56,6 kN
106,4 kN
Determine, de acordo com a ABNT NBR 8800:2008, o esforço normal de compressão resistente de cálculo (Nd,res) para a coluna soldada (CS) indicada na figura abaixo, cujo comprimento (L) é de 4,5 m. A coluna é simplesmente apoiada em relação aos dois eixos de análise.
Aço A-36 (MR250) – Propriedades: fy = 25 kN/cm2; fu = 40 kN/cm2; E = 20000 kN/cm2.
Perfil CS 650x345 kg/m – Propriedades:
d = 650 mm
h = 600 mm
tw = 19,0 mm
tf = 25,0 mm
bf = 650 mm

Em caso de resposta decimal, arredondar o número conforme o inteiro mais próximo.
Nd,res = 13660 kN
Nd,res = 9572 kN
Nd,res = 15295 kN
Nd,res = 8270 kN
Nd,res = 12873 kN
Determine, de acordo com a ABNT NBR 8800:2008, o esforço normal de compressão resistente de cálculo (Nd,res) para a coluna soldada (CS) indicada na figura abaixo, cujo comprimento (L) é de 3 m. A coluna é simplesmente apoiada em relação aos dois eixos de análise.
Aço A-36 (MR250) Propriedades: fy = 25 kN/cm2; fu = 40 kN/cm2; E = 20000 kN/cm2.
Perfil CS 700x458 kg/m Propriedades:
d = 700 mm
h = 637 mm
tw = 22,4 mm
tf = 31,5 mm
bf = 700 mm

Em caso de resposta decimal, arredondar o número conforme o inteiro mais próximo.
Nd,res = 13060 kN
Nd,res = 15780 kN
Nd,res = 10147 kN
Nd,res = 14373 kN
Nd,res = 12032 kN
Calcular a resistência de projeto (Rd) ao corte da ligação com parafuso de 19 mm diâmetro, que liga duas peças tracionadas de madeira eucalipto citriodora, conforme recomendações da ABNT NBR 7190:1997. Considerar classe de carregamento de longa duração, classe 2 de umidade e madeira serrada de 2ª categoria. Atribuir o valor característico da resistência à compressão paralela às fibras (fc0,k) do eucalipto critiodora como 43,4 MPa, e o valor característico da resistência ao escoamento do parafuso como 240 MPa.
Adotar:
d = 19 mm.
t1 = 40 mm.
t2 = 60 mm.

Nd,res = 122,9 kN.
Nd,res = 57,6 kN.
Nd,res = 144,3 kN.
Nd,res = 172,8 kN.
Nd,res = 49,2 kN.
Calcular as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça de madeira submetida à solicitação axial de tração, cujo esforço é originado a partir das seguintes ações características:
Peso próprio da estrutura de madeira: G = 21 kN (grande variabilidade)
Carga acidental (de uso e ocupação): Q = 25 kN
Ação do vento de sobrepressão: Qv1 = 17 kN
Ação do vento de sucção: Qv2 = -12 kN
Considerar que, na construção, há predominância de pesos e de equipamentos que permanecem fixos por longos períodos de tempo.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)?
76,3 kN
97,3 kN
124,5 kN
56,6 kN
106,4 kN
Determine, de acordo com a ABNT NBR 8800:2008, o esforço normal de compressão resistente de cálculo (Nd,res) para a coluna soldada (CS) indicada na figura abaixo, cujo comprimento (L) é de 4,5 m. A coluna é simplesmente apoiada em relação aos dois eixos de análise.
Aço A-36 (MR250) – Propriedades: fy = 25 kN/cm2; fu = 40 kN/cm2; E = 20000 kN/cm2.
Perfil CS 650x345 kg/m – Propriedades:
d = 650 mm
h = 600 mm
tw = 19,0 mm
tf = 25,0 mm
bf = 650 mm

Em caso de resposta decimal, arredondar o número conforme o inteiro mais próximo.
Nd,res = 13660 kN
Nd,res = 9572 kN
Nd,res = 15295 kN
Nd,res = 8270 kN
Nd,res = 12873 kN
Determine, de acordo com a ABNT NBR 8800:2008, o esforço normal de compressão resistente de cálculo (Nd,res) para a coluna soldada (CS) indicada na figura abaixo, cujo comprimento (L) é de 3 m. A coluna é simplesmente apoiada em relação aos dois eixos de análise.
Aço A-36 (MR250) Propriedades: fy = 25 kN/cm2; fu = 40 kN/cm2; E = 20000 kN/cm2.
Perfil CS 700x458 kg/m Propriedades:
d = 700 mm
h = 637 mm
tw = 22,4 mm
tf = 31,5 mm
bf = 700 mm

Em caso de resposta decimal, arredondar o número conforme o inteiro mais próximo.
Nd,res = 13060 kN
Nd,res = 15780 kN
Nd,res = 10147 kN
Nd,res = 14373 kN
Nd,res = 12032 kN
Calcular a resistência de projeto (Rd) ao corte da ligação com parafuso de 19 mm diâmetro, que liga duas peças tracionadas de madeira eucalipto citriodora, conforme recomendações da ABNT NBR 7190:1997. Considerar classe de carregamento de longa duração, classe 2 de umidade e madeira serrada de 2ª categoria. Atribuir o valor característico da resistência à compressão paralela às fibras (fc0,k) do eucalipto critiodora como 43,4 MPa, e o valor característico da resistência ao escoamento do parafuso como 240 MPa.
Adotar:
d = 19 mm.
t1 = 40 mm.
t2 = 60 mm.

76,3 kN
97,3 kN
124,5 kN
56,6 kN
106,4 kN
Determine, de acordo com a ABNT NBR 8800:2008, o esforço normal de compressão resistente de cálculo (Nd,res) para a coluna soldada (CS) indicada na figura abaixo, cujo comprimento (L) é de 4,5 m. A coluna é simplesmente apoiada em relação aos dois eixos de análise.
Aço A-36 (MR250) – Propriedades: fy = 25 kN/cm2; fu = 40 kN/cm2; E = 20000 kN/cm2.
Perfil CS 650x345 kg/m – Propriedades:
d = 650 mm
h = 600 mm
tw = 19,0 mm
tf = 25,0 mm
bf = 650 mm

Em caso de resposta decimal, arredondar o número conforme o inteiro mais próximo.
Nd,res = 13660 kN
Nd,res = 9572 kN
Nd,res = 15295 kN
Nd,res = 8270 kN
Nd,res = 12873 kN
Determine, de acordo com a ABNT NBR 8800:2008, o esforço normal de compressão resistente de cálculo (Nd,res) para a coluna soldada (CS) indicada na figura abaixo, cujo comprimento (L) é de 3 m. A coluna é simplesmente apoiada em relação aos dois eixos de análise.
Aço A-36 (MR250) Propriedades: fy = 25 kN/cm2; fu = 40 kN/cm2; E = 20000 kN/cm2.
Perfil CS 700x458 kg/m Propriedades:
d = 700 mm
h = 637 mm
tw = 22,4 mm
tf = 31,5 mm
bf = 700 mm

Em caso de resposta decimal, arredondar o número conforme o inteiro mais próximo.
Nd,res = 13060 kN
Nd,res = 15780 kN
Nd,res = 10147 kN
Nd,res = 14373 kN
Nd,res = 12032 kN
Calcular a resistência de projeto (Rd) ao corte da ligação com parafuso de 19 mm diâmetro, que liga duas peças tracionadas de madeira eucalipto citriodora, conforme recomendações da ABNT NBR 7190:1997. Considerar classe de carregamento de longa duração, classe 2 de umidade e madeira serrada de 2ª categoria. Atribuir o valor característico da resistência à compressão paralela às fibras (fc0,k) do eucalipto critiodora como 43,4 MPa, e o valor característico da resistência ao escoamento do parafuso como 240 MPa.
Adotar:
d = 19 mm.
t1 = 40 mm.
t2 = 60 mm.


Nd,res = 13660 kN
Nd,res = 9572 kN
Nd,res = 15295 kN
Nd,res = 8270 kN
Nd,res = 12873 kN
Determine, de acordo com a ABNT NBR 8800:2008, o esforço normal de compressão resistente de cálculo (Nd,res) para a coluna soldada (CS) indicada na figura abaixo, cujo comprimento (L) é de 3 m. A coluna é simplesmente apoiada em relação aos dois eixos de análise.
Aço A-36 (MR250) Propriedades: fy = 25 kN/cm2; fu = 40 kN/cm2; E = 20000 kN/cm2.
Perfil CS 700x458 kg/m Propriedades:
d = 700 mm
h = 637 mm
tw = 22,4 mm
tf = 31,5 mm
bf = 700 mm

Em caso de resposta decimal, arredondar o número conforme o inteiro mais próximo.
Nd,res = 13060 kN
Nd,res = 15780 kN
Nd,res = 10147 kN
Nd,res = 14373 kN
Nd,res = 12032 kN
Calcular a resistência de projeto (Rd) ao corte da ligação com parafuso de 19 mm diâmetro, que liga duas peças tracionadas de madeira eucalipto citriodora, conforme recomendações da ABNT NBR 7190:1997. Considerar classe de carregamento de longa duração, classe 2 de umidade e madeira serrada de 2ª categoria. Atribuir o valor característico da resistência à compressão paralela às fibras (fc0,k) do eucalipto critiodora como 43,4 MPa, e o valor característico da resistência ao escoamento do parafuso como 240 MPa.
Adotar:
d = 19 mm.
t1 = 40 mm.
t2 = 60 mm.


Nd,res = 13060 kN
Nd,res = 15780 kN
Nd,res = 10147 kN
Nd,res = 14373 kN
Nd,res = 12032 kN
Calcular a resistência de projeto (Rd) ao corte da ligação com parafuso de 19 mm diâmetro, que liga duas peças tracionadas de madeira eucalipto citriodora, conforme recomendações da ABNT NBR 7190:1997. Considerar classe de carregamento de longa duração, classe 2 de umidade e madeira serrada de 2ª categoria. Atribuir o valor característico da resistência à compressão paralela às fibras (fc0,k) do eucalipto critiodora como 43,4 MPa, e o valor característico da resistência ao escoamento do parafuso como 240 MPa.
Adotar:
d = 19 mm.
t1 = 40 mm.
t2 = 60 mm.

